Merge Sort Algorithm

Difficulty Level

Medium

Asked In

Microsoft, Amazon, Goldman Sachs, Qualcomm, Bloomberg, Oracle, Paytm

Merge Sort Introduction

Merge sort is one of the popular algorithms which uses a divide and conquer approach of problem-solving to sort an array(or list) of integers(or characters or strings). Here are some of the good reasons to learn this algorithm —

• One of the best algorithms to visualize recursion in programming. Its recursive structure and the base case are intuitive.
• One of the efficient comparison-based sorting algorithms that work in O(nlogn) time complexity in the worst case.
• We use a similar approach to solve other coding interview problems.
• A best sorting algorithm for sorting linked lists.
• One of the best algorithms to understand the recursion analysis using the recursion tree method and master theorem.
• The merging process of the merge sort is a good idea to learn problem-solving using two pointer approaches and extra memory. We use a similar approach to solve other coding interview problems.

Merge Sort Idea

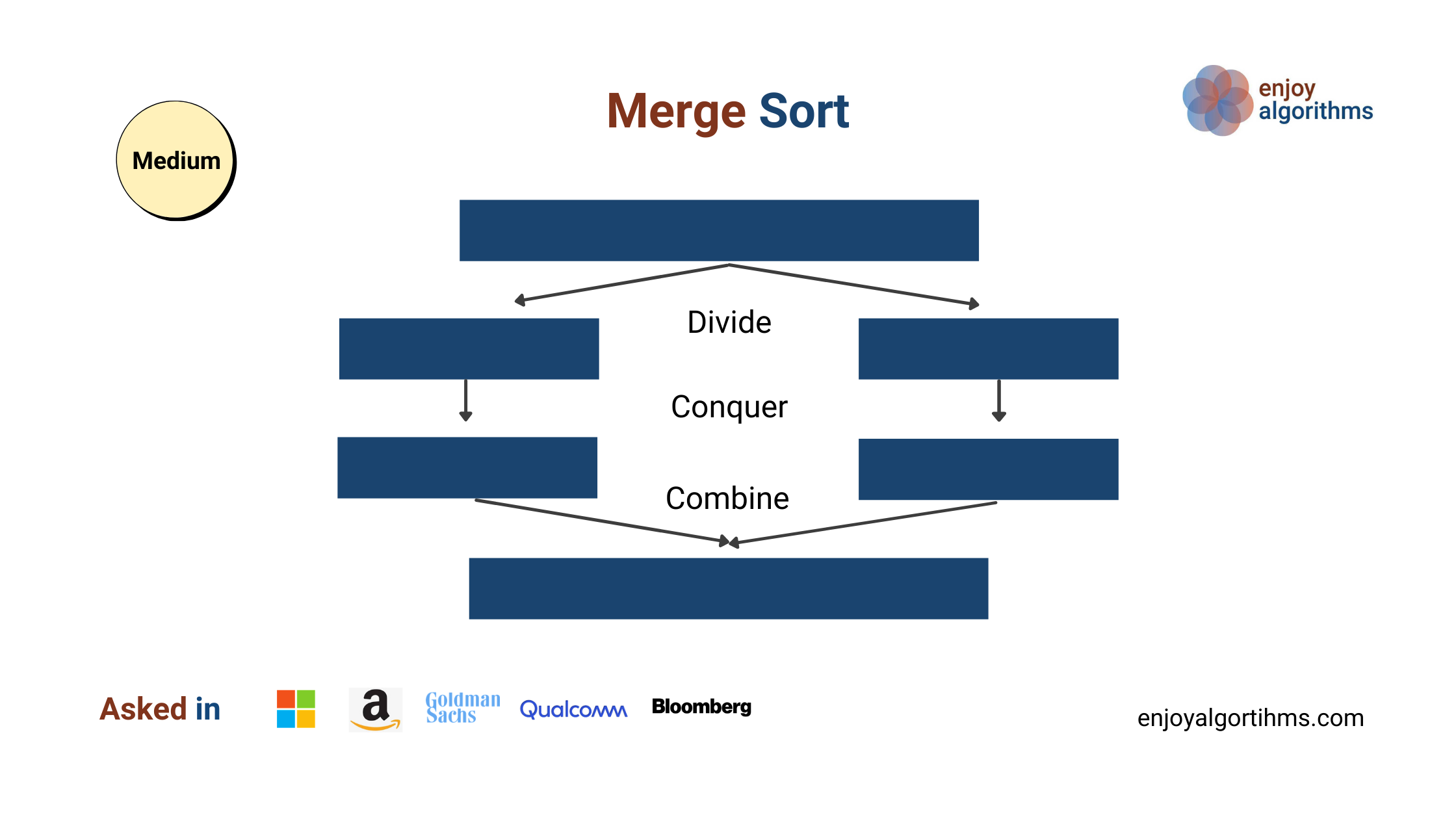
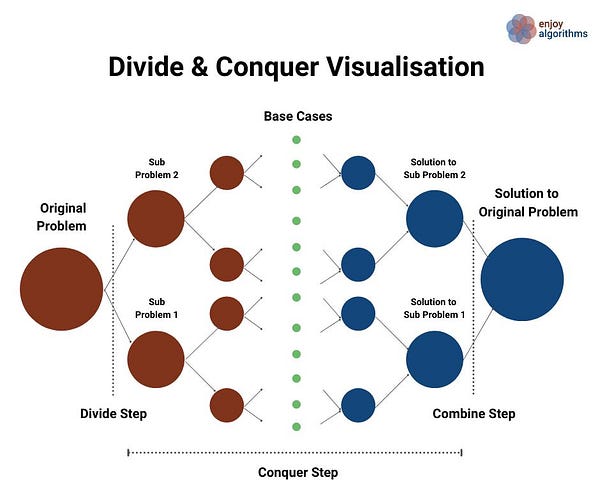
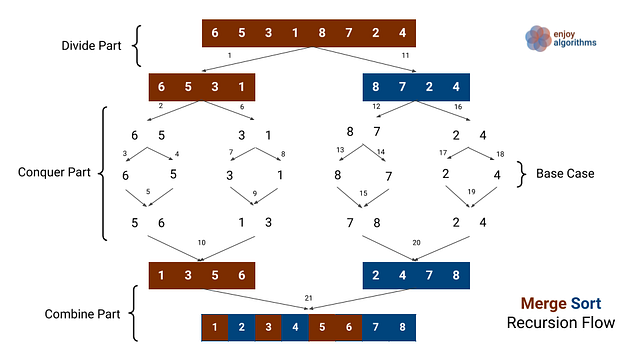
Suppose we have to write a program to sort an array A[l…r] of n integers starting from index l and ending at index r. Now the critical question is — how do we solve sorting using the solution of smaller sub-problems? Is there a scope to apply the divide and conquer approach? Let's think and understand via the following diagram.

If we observe from the above diagram, the flow of the divide and conquer algorithm will go like this —

Divide part— We divide the sorting problem of size n into two different and equal sorting sub-problems of size n/2. We can divide the problem by calculating the mid-value.

• Subproblem 1 — Sorting array A[] from l to mid
• Subproblem 2 — Sorting array A[] from mid+1 to r

Conquer Part — Now, we solve both the sub-problems recursively. We should not worry about the solutions to the two sub-problems because recursion will do the rest of the work for us.

Combine Part — We combine the solution of both the sub-problems to solve the original sorting problems. In simple words, we merge both sorted halves to generate the final sorted array. How? Think!

Merge Sort Steps

Suppose the function mergeSort(int A[], int l, int r) sort the entire array A[] where we are passing the left index and right index as an input parameter.

• Divide Part : Calculating the mid-value, mid = l + (r - l)/2
• Conquer Part 1: Recursively calling mergeSort(A, l, mid) to sort the left part. We are passing mid as the right index.
• Conquer Part 2: Recursively calling mergeSort(A, mid+1, r) to sort the right part. We are passing mid +1 as the left index.
• Combine Part: We use the function merge(A, l, mid, r) inside the function mergeSort() to merge both the sorted halves into a single sorted array.
• Base Case: If we find l≥r during the recursive calls, then the sub-array has at most one element left, which is already sorted. Our recursion should not go further and return from here. In other words, The sub-array of size one is the base condition.

Merge sort pseudo-code

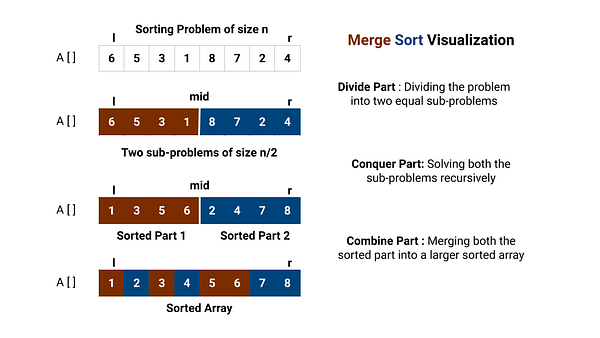
Merge Sort Visualisation

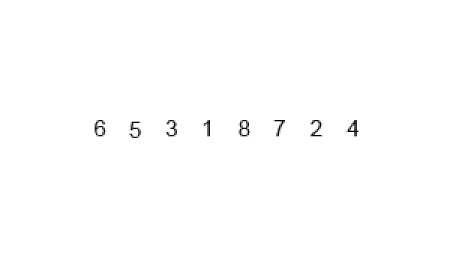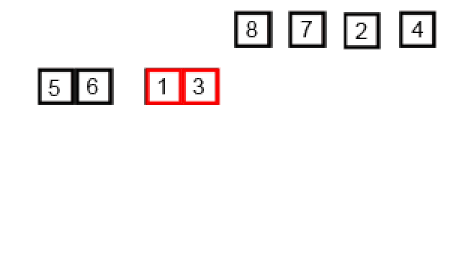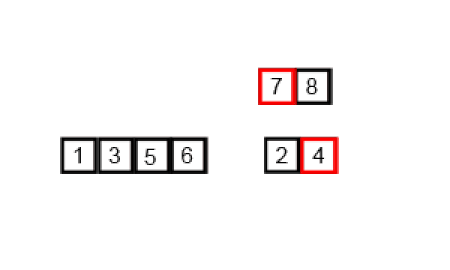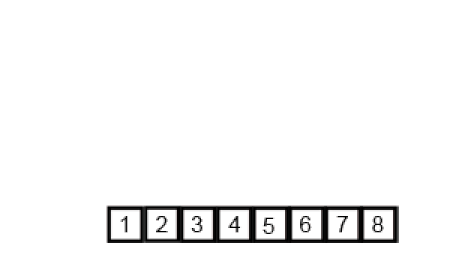
Combine Part — The idea of the Merging Process

After the conquer step, both left part A[l…mid] and right part A[mid+1…r] are recursively sorted. Now we need to combine the solution of the two smaller sub-problem to create the solution of the larger problem i.e. merge two sorted arrays to create a larger sorted array. How can we do it? Let’s think. But one thing is sure — we cannot merge these two sorted parts in-place or without using extra space. (Think!)

Here are some key ideas

• If we store the values of both sorted halves of A[] into two extra arrays of size n/2 (X[] and Y[]), then we can transform the problem into — merging sorted arrays X[] and Y[] to the larger sorted array A[]. For merging two sorted arrays, the most critical information is — Both the arrays are sorted.
• Using the sorted order property, we can compare the values one by one in both the arrays and incrementally build the solution or larger array sorted.
• How we implement it? The idea is — we can use two separate pointers i and j to traverse the array X[] and Y[] from the start. During the traversal, we compare elements in X[] and Y[] and place a smaller value to the larger array A[], and increase the pointer in the smaller array from which the value is coming from. (Think!)
• Another analogy would be — we can build the partial solution incrementally by comparing the values in both the smaller array. After each comparison, we can add one input to the output and build the partially sorted array A[].

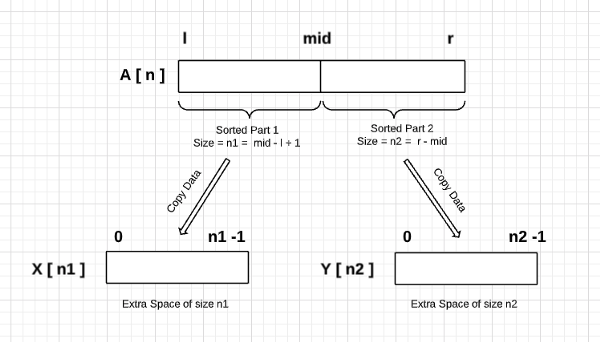
Step 1— Memory allocation and data copy process

• Calculating the size of both left and right sorted parts. Size of left part (n1) = mid - l +1, Size of right part (n2) = r - mid . We include the value stored at the mid-index on the left part.
• We allocate the extra space of sizes n1 and n2 to store the left and right sorted part — X [n1] and Y [n2].
• We copy the data stored in both the left and right parts of array A[] into the array X[ ] and Y [ ], respectively.

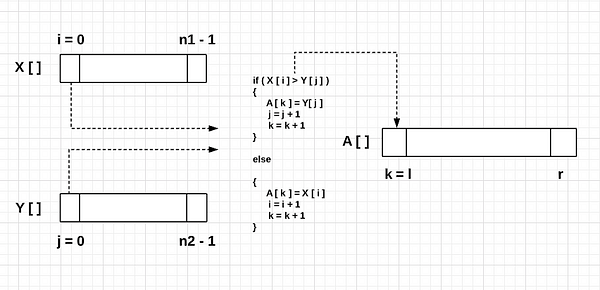
Step 2 — Loop Initialization

• We initialises the loop pointers i, j, and k to traverse the array X[], Y[], and A[] respectively during the merging process i.e. i = 0, j = 0 and k = l. Since i = j =0, X[i] and Y[j] are the smallest elements of their arrays.
• Now we run a loop until any one of the smaller arrays reaches its end. while(i < n1 and j < n2).
• At the first step of the iteration, we need to store the smallest value to the first position of A[]. For this, We compare the X[i] and Y[j] and place smaller values at A[k].
• Now we need to place the second smallest element in the next iteration. But before this, we need to increment the pointer k in A[] and pointer in the array containing the smaller value(It may be i or j, which depends on the comparison). Think!

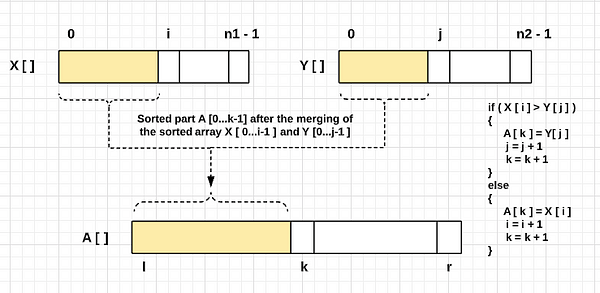
Step 3— Loop Maintenance 

• Like the first iteration, we move forward in all three arrays using pointers i, j, and k. At each step, we are comparing X[i] & Y[j], placing a smaller value to A[k], and incrementing the value of k by 1. We are also incrementing the pointers i and j on the based on the comparison.
• In other words, at each step of the iteration, we are building the partial solution and adding one value to the larger array A[] (Think!).
• This is a two-pointer approach to solving a problem by building a partial solution. Here both pointer i and j are moving in the same direction.

Step 4— Loop Termination and building the final solution

• When any one of the pointer i and j reaches its end (either i=n1 or j = n2), then we should exit the loop because we can’t apply the above loop idea in such a situation.
• Boundary Case 1— If we exit the loop due to condition i = n1, then we reached the end of the sorted array X[] or, we have placed all the values of X[] in A[]. But there may be some values remaining in Y[] to place in the larger sorted array. The idea is simple— we should copy all the remaining values of Y[] in the larger array A[].

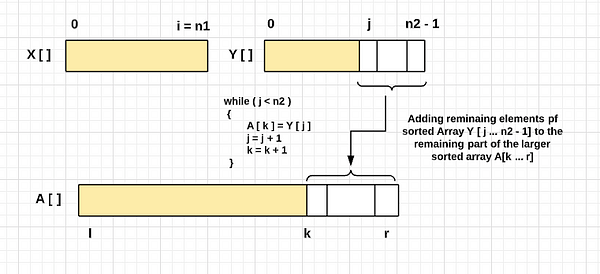
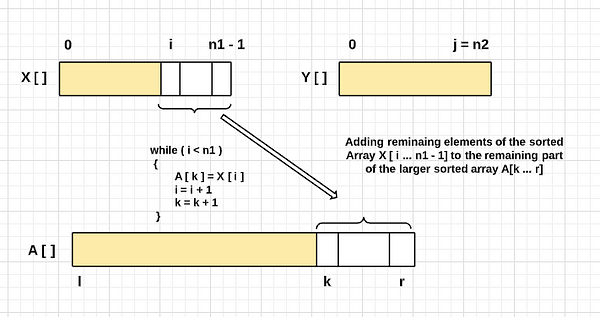
• Boundary Case 2— If we exit the loop due to condition j = n2, then we reached the end of the sorted array Y[], or we have placed all the values of Y[] in A[]. But there may be some values remaining in X[] to put in the larger sorted array. The idea is simple — we should copy all the remaining values of X[] in the larger array A[].

Pseudocode of the Merging Process

Analysis of the Merging Process

This is an excellent code to understand the time complexity of the iterative approach. To understand this better, let's calculate each critical process's time complexity and do the summation to calculate the overall time complexity.

• Memory Allocation = O(1)
• Data Copy Process = O(n1) + O(n2) = O(n1+n2) = O(n)
• Inner while loop (In the worst case) = O(n1 + n2) = O(n) (Think!)
• Boundary condition 1(In the worst case) = O(n1) (Think!)
• Boundary condition 2(In the worst case) = O(n2) (Think!)

Overall Time Complexity = O(1)+ O(n) + O(n) + O(n1) + O(n2) = O(n)

If we observe closely, then the merging process's time complexity will be dependent on the inner while loop where comparison, assignment, and increment are the key operations. If we try to analyse it, there may be two different approaches.

• Approach 1 — At each step of the while loop, we are incrementing either pointer i or j. In the worst situation, we have to traverse both the arrays until the end. It means the total number of loop operations in the worst case = O(n1) + O(n2) = O(n1 + n2) = O(n).
• Approach 2— We are placing each element of the smaller sorted arrays to the larger array A[]. It will take O(1) or constant time for adding each value. Time complexity = (n1 + n2) * O(1) = n*O(1) = O(n)

Analysis of the Merge Sort

Let's assume that T(n) is the worst-case time complexity of merge sort on n integers. Merge sort on a single element takes constant time. When we have n>1, then we can break down the time complexities as follows —

• Divide Part — The time complexity divide part is O(1) because this step calculates the middle index of the array, which takes constant time.
• Conquer Part— We are recursively solving two sub-problems, each of size n/2. So the time complexity of each subproblem is T(n/2) and the overall time complexity of the conquer part is 2T(n/2).
• Combine Part — As calculated above, the worst-case time complexity of merging is O(n).

For calculating the T(n), we need to add the time complexities of the divide, conquer, and combine part => T(n) = O(1) + 2 T(n/2) + O(n) = 2 T(n/2) + O(n) = 2 T(n/2) + cn

So the recurrence relation of the worst-case time complexity, where constant c represents the time required to solve the problem of size 1.

• T (n) = c, if n = 1
• T(n) = 2 T(n/2) + cn, if n > 1

Note: Our merge sort function works correctly when the number of elements is not even. But to simplify the analysis, we assume that input size n is a power of 2 where the divide step creates the sub-problems of size exactly n/2. This assumption does not affect the order of growth of the analysis. (Think!)

Using the recursion tree method

In this method, we draw a recursion tree and calculate the time taken by every level of the tree. Finally, we find the overall time complexity by doing the sum of time taken at all levels.

Analysis of merge sort using the master theorem

Master Method is a direct way to get the solution for the recurrences that can be transformed to the following type:

T(n) = aT(n/b) + f(n) where a≥1 and b>1

There are the following three cases of the solution:

• If f(n) = O(n^k) where k<logb(a) then T(n) = O(n*logb(a))
• If f(n) = O(n^k) where k = logb(a) then T(n) = O(n^k * logn)
• If f(n) = O(n^k) where k > logb(a) then T(n) = O(f(n))

Now we compare the above recurrence with the merge sort recurrence

• T (n) = c, if n = 1
• T(n) = 2 T(n/2) + cn, if n > 1

Here a = 2, b = 2, f(n) = cn where both a≥1 and b>1. So we can apply the master theorem to solve it.

=> f(n) = cn = cn¹ = O(n¹) => k = 1,

=> Similarly, logb(a) = log 2(2) = 1

=> Hence logb(a) = k = 1

It means, Merge sort recurrence satisfy the 2nd case of the master theorem. Then solution T(n) = O(n^k * log n) = O(n^1 * lon n) = O(nlog n)

Some Important Properties of Merge Sort

• Merge sort is a stable sorting algorithm which means that the order of equal elements are same in the input and output.
• We can parallelise the implementation of the merge sort well due to the use of the divide-and-conquer method, where every smaller sub-problem is independent of each other.
• The multiway merge sort algorithm is very scalable through its high parallelisation capability, which allows many processors. This makes the algorithm a viable candidate for sorting large amounts of data, such as those processed in computer clusters. Also, since memory is usually not a limiting resource in such systems, the disadvantage of space complexity of merge sort is negligible.
• Merge sort is the best choice for sorting a linked list. In this situation, it is relatively easy to implement a merge sort to require only Θ(1) extra space. On another side, the slow random-access performance of a linked list makes some other algorithms such as quicksort perform poorly and others like heap sort completely impossible.
• For the smaller input, It is slower in comparison to other sorting algorithms. Even it goes through the complete process if the array is already or almost sorted.
• We can implement merge sort iteratively without using an explicit auxiliary stack. On another side, recursive merge sort uses function call stack to store intermediate values of function parameters l and r and other information. The iterative merge sort works by considering window sizes in exponential oder, i.e., 1,2,4,8..2^n over the input array. For each window of any size k, all adjacent pairs of windows are merged into a temporary space, then put back into the array. Explore and Think! We will write a separate blog on this.

Similar Coding Interview Problems

• Find inversion count of an array
• External sorting algorithm
• Recursive algorithm of the maximum sub-array sum
• Recursive algorithm of finding max and min in an array
• Merge sort with O(1) extra space

Enjoy learning, Enjoy coding, Enjoy algorithms!