Find equilibrium index of an array

Difficulty Level

Easy

Asked In

Amazon, Adobe, Hike

Three solutions Discussed

1. Brute force approach — Using two nested loops
2. Using extra space — Using prefix sum array
3. An efficient approach— Using a single scan

Key takeaway after reading this blog

This is a good coding interview problem to learn — how to optimize space complexity and solve the problem using a single scan. We can find a lot of similar problems asked during the coding interview.

Let’s understand the problem

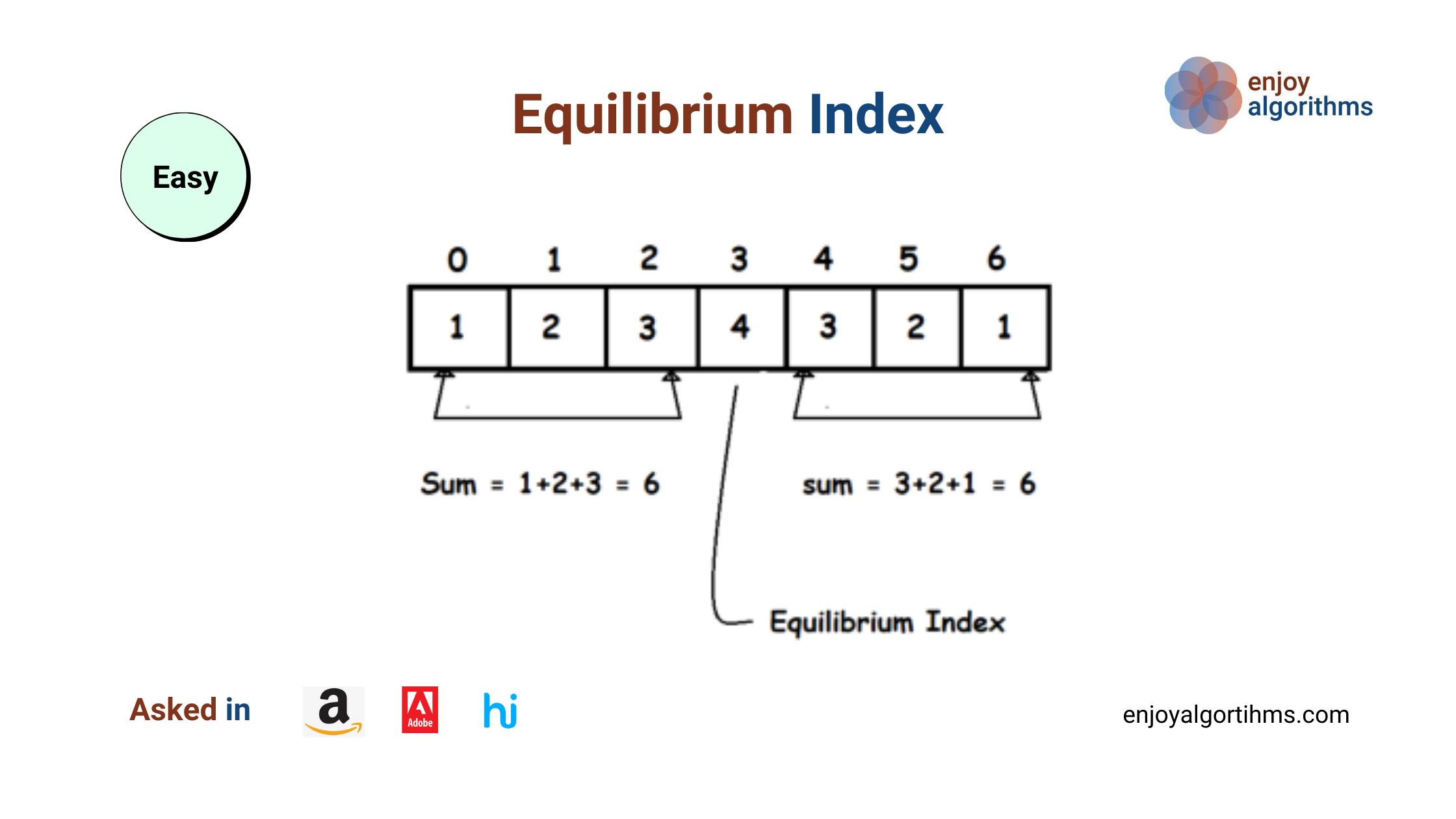
Write a program to find the equilibrium index of an array. The equilibrium index of an array is an index such that sum of elements at lower indexes equal to the sum of elements at higher indexes.

• In other words, the equilibrium index of an array is an index i such that the sum of elements at indices less than i is equal to the sum of elements at indices greater than i. Element at index i is not included in either part.

  A[0] + A[1]+….. + A[i-1] = A[i+1] + ….. + A[n-1], Where 0 < i < n-1

• It is stated that at max there is only one equilibrium index in the array. Return the index if it is present otherwise return -1.

• Values in the input array can be repeated.

  Example 1

  Input: A[] = [-7, 1, 5, 2, -4, 3, 0] 
  Output: 3
  Explanation: 3 is an equilibrium index 
  A[0] + A[1] + A[2] = A[4] + A[5] + A[6]
  

  Example 2

  Input: A[] = [0, 1, 3, -2, -1]
  Output: 1
  Explanation: 1 is an equilibrium index, 
  A[0] = A[2] + A[3] + A[4]
  

Brute force approach — Using two nested loops

Algorithm Idea

A straightforward method is to use two loops. The idea is to find the sum of elements for every range of indexes and observe if there exists an equilibrium index. The outer loop traverses the array, and the inner loop determines if there is an equilibrium index or not.

Algorithm Steps

1. Run a loop through the array.
2. For each index, find the sum of elements towards the left and right of the current index.
3. If the leftSum and rightSum are equal, then the current index is the equilibrium index.
4. Otherwise, return -1.

Algorithm Pseudocode

Algorithm Analysis

We are running nested loops and calculating leftsum and rightsum for every value of i. Total number of summation operation = n(n-1) (Think!)

Time Complexity = O(n²), Space Complexity: O(1)

Using extra space — Using prefix sum array

Algorithm Idea

The idea is to store the prefix sum of the array. The prefix sum would help keep track of the sum of all elements up to any index of the array. Now, we should find a way to keep track of the sum of values to the right of the current index. We can use a temporary sum variable, which initially stores the sum of all elements of the array. If we subtract the value at the current index, we will get the sum of values to the right. Now, compare both leftSum and rightSum to find whether the current index is the equilibrium index or not.

Algorithm Steps

1. Store prefix sum of the array using extra space.
2. Get the total sum of the array as rightSum.
3. Now, iterate through the array and compare the leftSum and rightSum.
4. If leftSum equals rightSum, return the current index.
5. Otherwise, return -1.

Algorithm Pseudocode

Algorithm Analysis

We are running two separate loops for calculating the prefix sum array and equilibrium index respectively. Time Complexity = Time complexity of calculating prefix sum array + Time complexity of calculating Equilibrium Index = O(n) + O(n) = O(n)

Space Complexity: The above algorithm uses extra space to create a prefix sum array. Hence, the space complexity would be O(n).

An efficient approach - Using a single scan

Algorithm Idea

The motive is to get the total sum of the array first. The difference between the above method and this method is that we don’t need to store the prefix sum beforehand. Instead, we will keep track of the leftSum while traversing the array itself. In the loop, we can get the rightSum by subtracting the elements one by one.

Algorithm Steps

1. Store the total sum of the array as totalSum.
2. Iterate through the array and keep track of the leftSum by adding the value at the current index and rightSum by subtracting the value at the current index from totalSum.
3. If leftSum equals rightSum, return the current index.
4. Otherwise, return -1.

Algorithm Pseudocode

Algorithm Analysis

We are running two separate loops for calculating the total sum and equilibrium index respectively. Time complexity = Time complexity of calculating prefix sum array + Time complexity of calculating Equilibrium Index = O(n) + O(n) = O(n)

Space Complexity = O(1), because we are just using variables to store the value of total, left, and right sum.

Possible questions by the Interviewer

• Can we solve this problem using the hash table?
• Can we solve this problem using two pointer approach?
• How to modify the above code if there can be multiple equilibrium indexes? What would be the different corner cases?

Problems for practice using a single scan

• Remove duplicates from sorted array
• A Product Array Puzzle
• Valid Mountain
• Chocolate Distribution Problem
• Best Time to Buy and Sell Stock
• Partition the array into three equal sum segments
• Sort an array in the waveform
• The maximum difference between two elements such that larger element appears after the smaller number
• Number of jumps for a thief to cross walls
• Find the number of subarrays with even sum

Enjoy learning, Enjoy Thinking, Enjoy Algorithms!